STATISTICS with R
A comprehensive guide to statistical analysis in R
Spearman Correlation in R
The Spearman correlation is a statistical method that measures the strength and direction of the nonlinear relationship between two variables. Unlike Pearson correlation, which assesses linear relationships, Spearman correlation evaluates how well the variables maintain a consistent increasing or decreasing trend, regardless of exact linearity, using the ranks of the values in the two variables. The Spearman correlation coefficient (ρ) ranges from -1 to 1, where values near -1 or 1 indicate a strong correlation, and values close to zero suggest a weak or no correlation. Spearman correlation is particularly useful for ordinal data or for data that does not meet the assumptions of normality required by Pearson correlation, such as when there are outliers in the data because ranks are robust to outliers.
Introduction to Spearman Correlation
When there are several random variables in a study or a data set, some of those variables may be related to each other. As an example, suppose a health researcher collects data on the number of hours participants exercise and the amount of weight they lose. Common sense suggests that the more hours participants do exercises, the more weight they should lose. In other words, there is a correlation between the number of hours done exercising and the amount of weight shed. We can quantify this relationship between two variables using a correlation coefficient.
The statistical method used to quantify this relationship depends on the nature of the data, particularly the linearity assumption. A nonlinear relationship between two variables may occur if the rate of change in one variable is different from the rate of change in the other variable. A simple plot may show the existence of such nonlinear relationships. In addition, the distribution of the data may not be normal, which is a requirement for some linear correlation tests, such as Pearson test. In other cases, the data could be ordinal, such as ranking or rating produced by two raters on a writing test. One appropriate statistical test for nonlinear relationship between two random variables, or when the normality assumption is not met, is the Spearman rho correlation test.
Like other common correlation coefficients, the Spearman rho test shows the strength of a correlation (ranging between -1 and +1). A correlation of 0 means the two variables are totally unrelated to each other. A positive correlation means that the values of both variables change together: either increasing together or decreasing together. However, if the values of one variable increase while the values of the other variable decrease, the correlation value will have a negative sign which means the two variables have opposite values.
In the following sections, we demonstrate an example of a nonlinear relationship between two random variables and provide R code to quantify the strength, direction, and the statistical significance of the nonlinear relationship.
Spearman Correlation Example
Is there a relationship between the number of hours individuals exercise and their weight loss?

A health researcher is interested to know if there is a relationship between how many hours individuals exercise (hours/week) and the amount of weight they lose (in six months). The health researcher recruits 43 participants who on a questionnaire indicated that they exercise weekly and how many hours a week. In addition, they recorded their initial body weight at the beginning and at the end of the study term (six months). Table 1 includes the number of weekly exercise hours and the amount of weight loss (in pounds) after six months for five participants in the study.
| Participant | Exercise Hours | Weight Loss (lb) /th> |
|---|---|---|
| Participant 1 | 2 | 1.6 |
| Participant 2 | 2.5 | 1.8 |
| Participant 3 | 2.5 | 1.8 |
| Participant 4 | 3 | 1.8 |
| Participant 5 | 3.5 | 2 |
| … | … | … |
The health researcher enters the data in a spreadsheet program in the computer and saves the data in the CSV format. The complete data set for this example can be downloaded from here.
Analysis: Spearman Correlation R
In the first step, the health researcher reads the data into the RStudio program using the read.csv() function. After reading in the data, the health researcher reviews the data set and decides to create two variables, one for the number of exercise hours studied (exerciseHours) and one for the weight loss (weightLoss).
Because the health researcher is interested in knowing the relationship between the number of exercise hours and the amount of weight loss, first she plots the data to observe any interesting patterns. So, she draws a scatter plot of the data to preview the relationship between Exercise hours and Weight loss, illustrated in Figure 1 below.
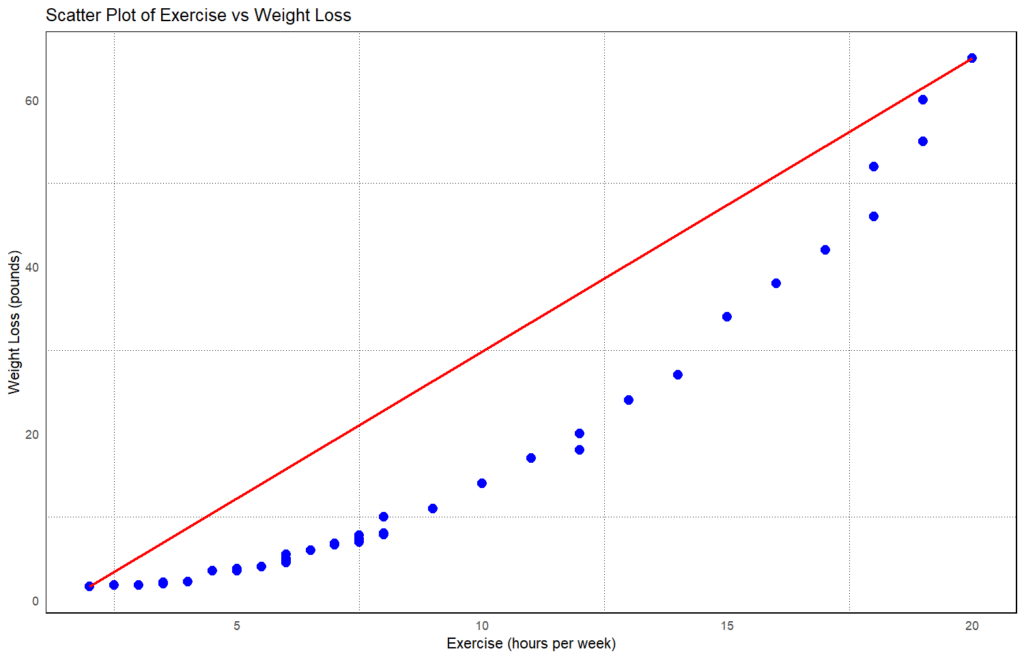
The health researcher realizes that although there is a relationship, the data points do not fall close to the red line, implying that the relationship is not linear. Therefore, to quantify this nonlinear relationship, the researcher decides to use Spearman rho correlation coefficient.
To calculate a Spearman rho correlation coefficient between the Exercise hours and Weight loss, we can use the cor.test() function in R. The cor.test() is a built-in R function, and therefore, we do not need to install and call a package to use this function. The following code in Listing 2 shows how to perform a Spearman rho correlation between two continuous random variables with nonlinear relationship.
> dfWeights <- read.csv("dsExerciseWeightLoss.csv")
> exerciseHours <- dfWeights$Exercise
> weightLoss <- dfWeights$WeightLoss
> corrHoursScores <- cor.test(exerciseHours, weightLoss,
method = "spearman",
alternative = "two.sided")
> print(corrHoursScores)
Spearman's rank correlation rho
data: exerciseHours and weightLoss
S = 24.034, p-value < 2.2e-16
alternative hypothesis: true rho is not equal to 0
sample estimates:
rho
0.9981853In this code, the parameters of the cor.test() function include the names of the two variables (Exercise hours and Weight loss), the statistical method (we asked for Spearman correlation because we observed that the relationship was nonlinear), and the null hypothesis (two-sided, which means we assume there is no relationship and hence rho = 0).
The results of the Spearman rho correlation in Listing 2 include the S value (sum of squared rank differences), the p-value, and the Spearman correlation coefficient rho (shown as sample estimates: rho). In this example, the Spearman rho correlation is 0.99, is positive, and is statistically significant. This implies that there is a very strong relationship between the number of weekly exercise hours and the amount of weight loss. In other words, the more time dedicated to exercise per week, the more weight individuals will lose in about six months.